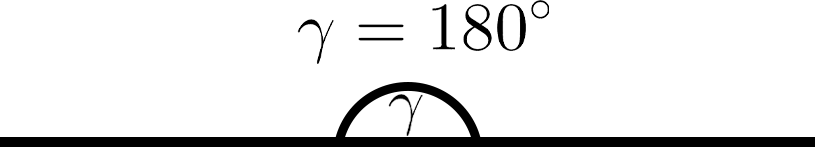Кунҷ
Зовия, гӯша ё кунҷ — яке аз шаклҳои ҳандаса мебошад, ки аз ду нури аз як нуқта барояндаро қуллаи кунҷ меноманд.
Маълумоти умумӣ

Ҳамворе ки ҳарду тарафи кунҷ дорад, аз рӯи кунҷ ба ду минтақа тақсим мешавад. Ҳар яке аз ин минтақаҳо, ки бо паҳлӯҳои кунҷ якҷоя мешаванд, кунҷи ҳамворӣ номида мешаванд (ё танҳо кунҷ, агар ин боиси нофаҳмиҳо нагардад). Яке аз кунҷҳои ҳамворӣ (одатан хурдтар аз ҳарду) баъзан ба таври шартӣ дохилӣ номида мешавад ва дигаре берунӣ.
Нишон додани кунҷ


Барои нишон додани кунҷ як аломати маъмулӣ мавҷуд аст: Соли 1634 аз ҷониби математики фаронсавӣ Пьер Херигон пешниҳод шудааст. Аломат дар Юникод мавҷуд аст (U+2220 ∠ кунҷ).
Дар ифодаҳои математикӣ кунҷҳо аксар вақт бо ҳарфҳои хурди юнонӣ ифода карда мешаванд: Шаблон:Math ва ғайра. Одатан, ин нишонаҳо инчунин ба расм истифода мешаванд, то норавшаниро дар интихоби майдони дохилии кунҷ бартараф созанд. Барои роҳ надодан ба иштибоҳ бо пӣ, рамзи Шаблон:Math одатан барои ин мақсад истифода намешавад. Барои ифода кардани кунҷҳои сахт (нигаред ба поён), ҳарфҳо аксар вақт истифода мешаванд Шаблон:Math ва Шаблон:Math.
Нишон додани кунҷ бо се аломати нуқта низ маъмул аст, масалан. Дар чунин сабт — боло, ва Ва — нуқтаҳое, ки дар паҳлӯҳои гуногуни кунҷ ҷойгиранд. Аз сабаби интихоби самти ҳисобкунии кунҷҳо ба муқобили ақрабаки соат дар математика, одат шудааст, ки нуқтаҳое, ки дар паҳлӯҳо ҷойгиранд, ҳангоми таъини кунҷ низ ба муқобили ақрабаки соат номбар карда шаванд. Ин конвенсия имкон медиҳад, ки ду кунҷи ҳамворӣ бо паҳлӯҳои умумӣ, вале минтақаҳои гуногуни дохилӣ фарқ кунанд.


Намудҳои кунҷҳо
-
Гӯшаи барҷаста
-
Кунҷи рост
-
Кунҷи пурра
-
Кунҷи шадид
-
Кунҷи ҳамвор
-
Кунҷи пурра
Биссектриса
Биссектриса (аз Шаблон:Lang-la «дугона» ва Шаблон:Lang-la2 «буриш») — шуоъест, ки аз қуллаи кунҷ берун меояд ва аз минтақаи дарунии он мегузарад, ки бо паҳлӯҳояш ду кунҷи баробар ташкил медиҳад.
Андозагирии кунҷҳо
Яке аз асбобҳои маъмултарин барои сохтан ва чен кардани кунҷҳо протрактор (инчунин ченак - ба поён нигаред) мебошад; чун қоида, барои сохтани кунҷи андозаи муайян истифода мешавад.
- (ниг. Функсияи хатӣ ; инчунин нигаред ба #Angle ва нуқтаи маҳсулот)
Эзоҳ
Ҳамчунин нигаред
Адабиёт
- Шаблон:Статья'
- Шаблон:Книга
- Шаблон:Книга
- Weisstein, Eric W. Line Bisector (англ.) на сайте Wolfram MathWorld.
- Weisstein, Eric W. Angle (англ.) на сайте Wolfram MathWorld.
- Weisstein, Eric W. Polygon (англ.) на сайте Wolfram MathWorld.
- Шаблон:Статья
- Шаблон:Статья